首页 计算机科学 R 语言

# 数据可视化

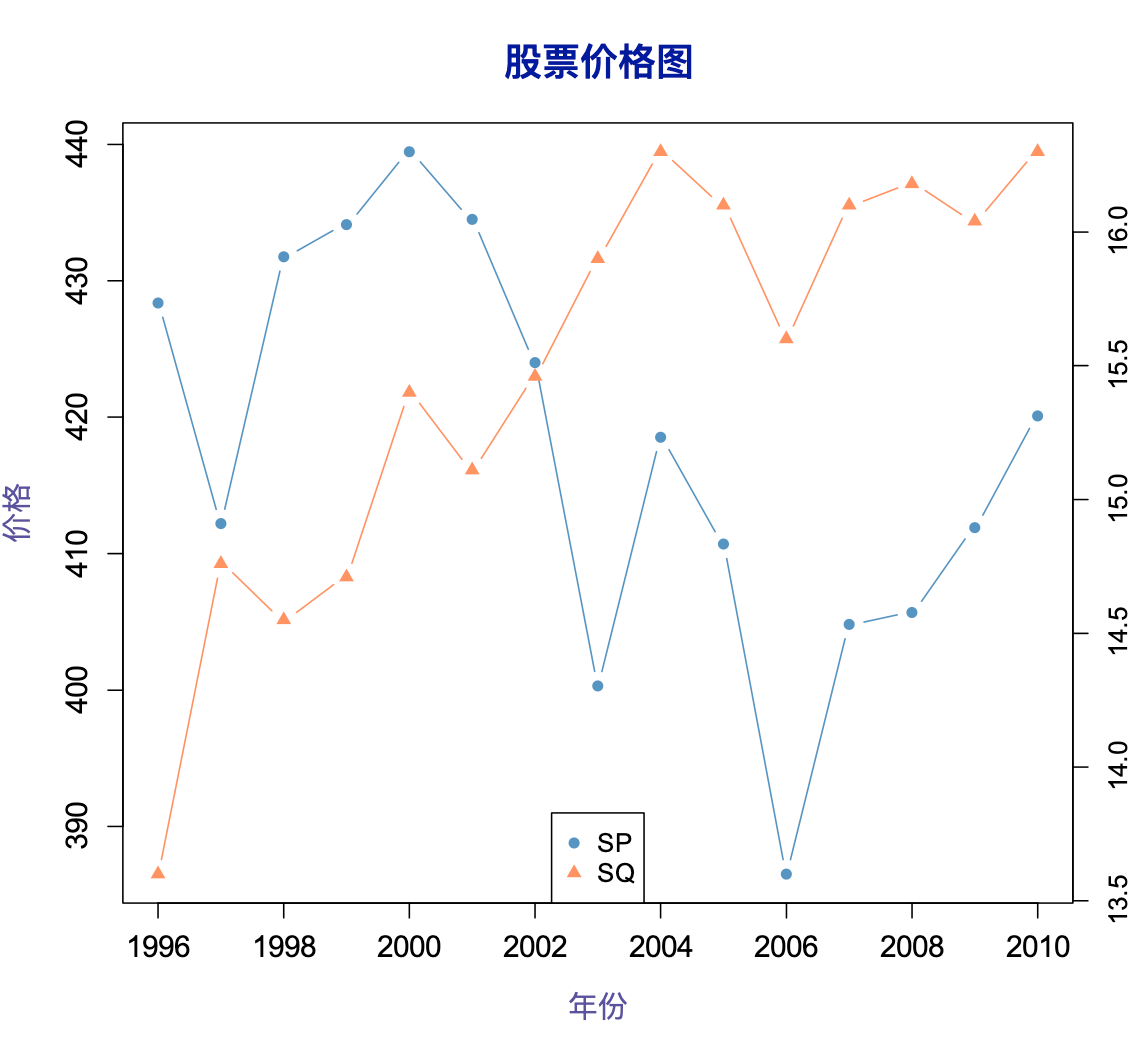
假设有 SP 和 SQ 两只股票在 1996～2010 年的年平均价格数据；
绘制左右两个不同刻度的 Y 轴，进行直观比较。
img.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# 实训：股票
library(readxl)
stock <- read_excel("251014/data/stock.xlsx", sheet = 1, col_names = TRUE)
ylim <- range(stock$SP, stock$SQ)  # y轴范围
# 绘制第一个股票的价格图
plot(stock$year, stock$SP, type = "b", pch = 16, col = "steelblue",
    main = "股票价格图", xlab = "年份", ylab = "价格",
    col.main = "darkblue", col.lab = "darkslateblue",
    cex.axis = 1.2, cex.lab = 1.2, cex.main = 1.5,
    font.lab = 3, font.main = 2)
par(new = T)    # 在原图上覆盖
# 绘制第二个股票的价格图
plot(stock$year, stock$SQ, type = "b", pch = 17,
    axes = FALSE, col = "coral",
    xlab = "", ylab = "", main = "")
# 创建新的y轴
axis(side = 4)
mtext("价格", side = 4, line = 3, col = "coral", cex = 1.2)

# 绘制图例
legend("bottom", legend = c("SP", "SQ"),
      col = c("steelblue", "coral"), pch = c(16, 17))

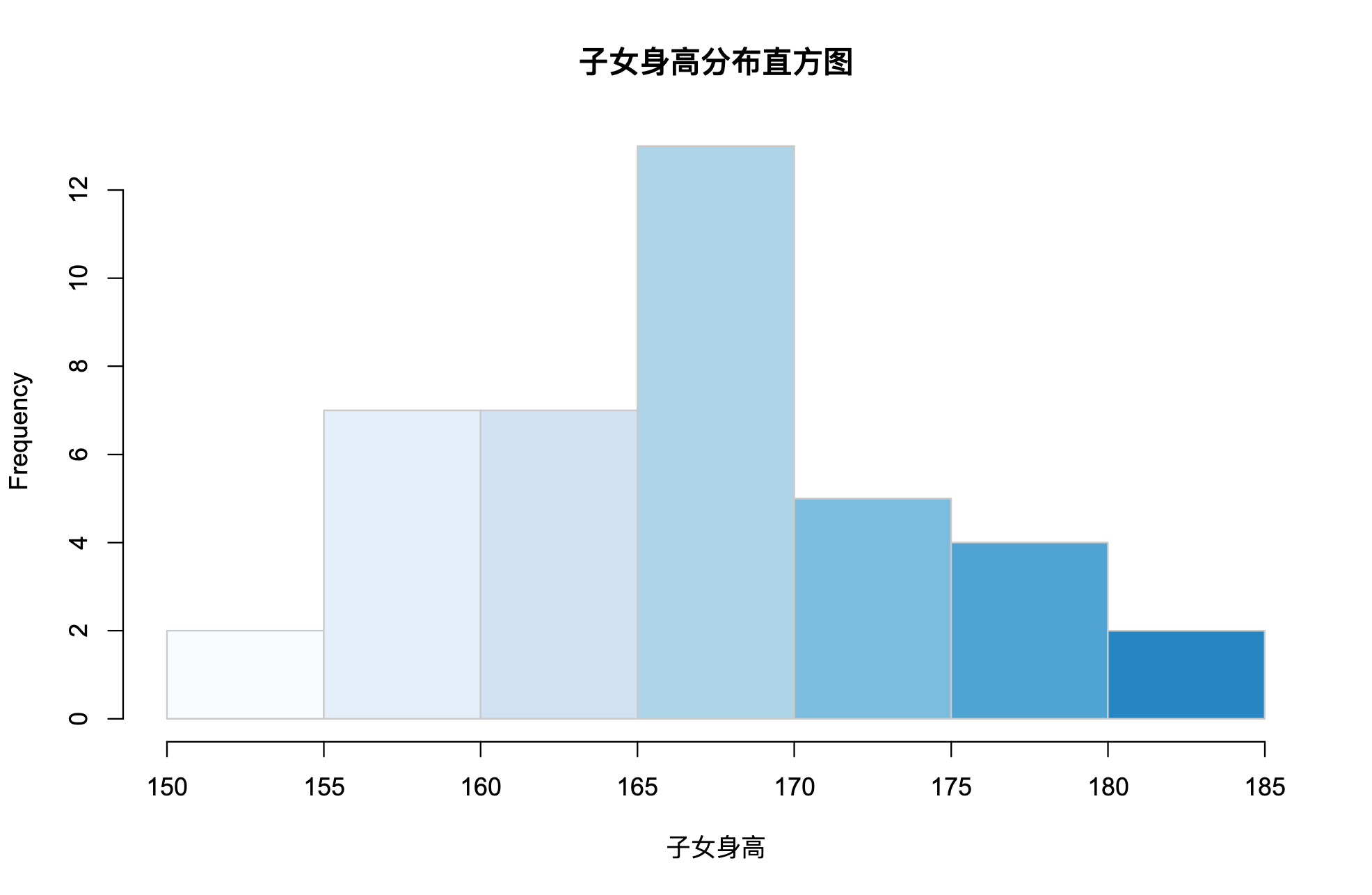
下面练习使用 exercise3_2 ，随机调查的 40 名学生及其父母的身高数据 (单位:cm)。

# 直方图

img.png

1
2
3
4
5
6
7
8
9
10
11
# 绘制children直方图，并用DescTools分析分布特征
hist(data$children,
     main = "子女身高分布直方图",
     xlab = "子女身高",
     col = brewer.pal(12, "Blues"),
     freq = TRUE,
     breaks = "FD",
     border = "gray")
     
# 使用DescTools提供的描述统计量分析
Desc(data$children)

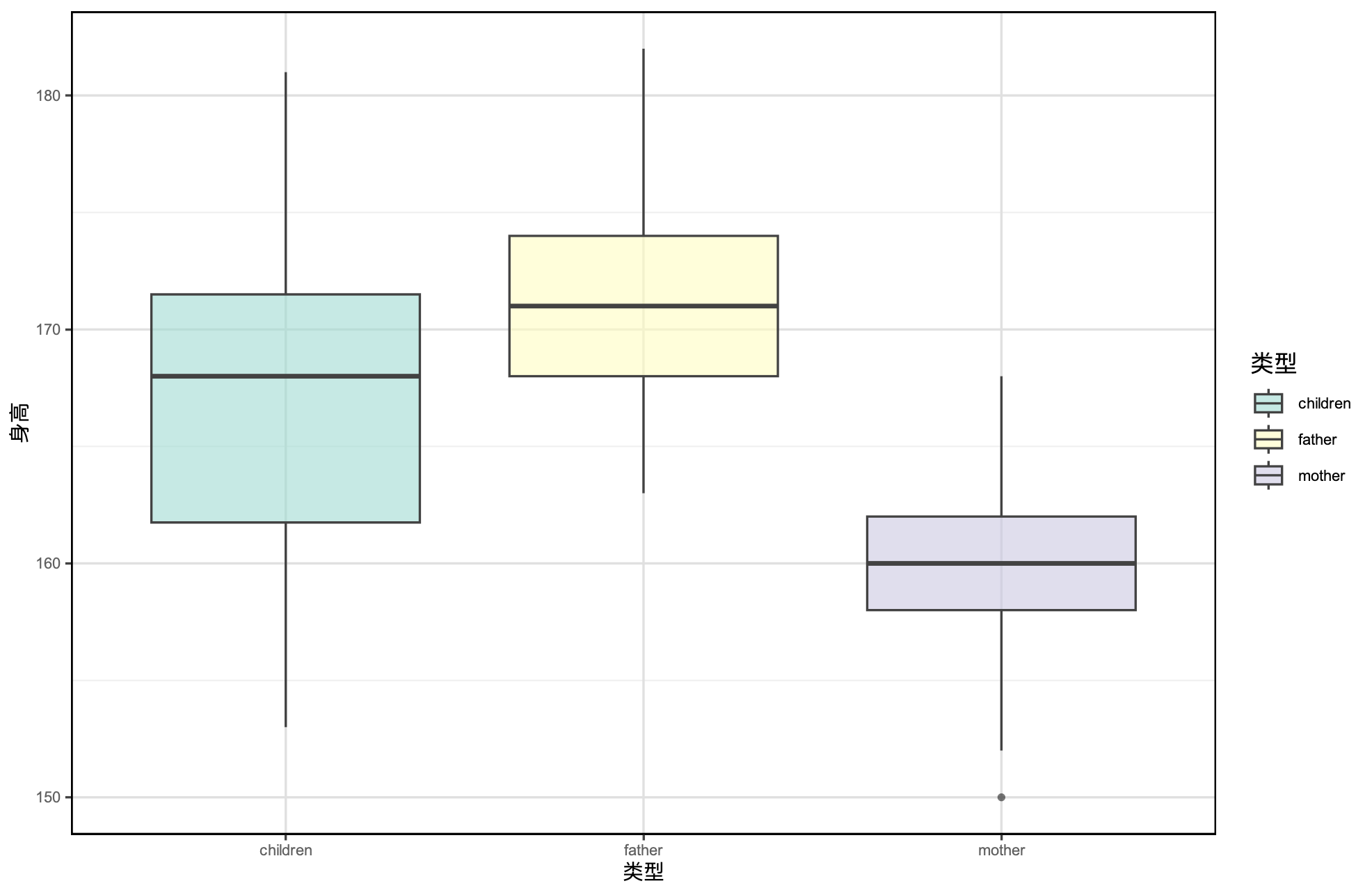
# 箱形图

img.png
绘制子女身高、父亲身高和母亲身高的箱形图，分析其分布特征。

1
2
3
4
5
6
7
data_long <- melt(data[, c("children", "father", "mother")],
                  variable.name = "类型", value.name = "身高")

ggplot(data_long, aes(x = 类型, y = 身高, fill = 类型)) +
  geom_boxplot(outlier.colour = "black", outlier.shape = 16, alpha = 0.6) +
  scale_fill_brewer(palette = "Set3") +
  mytheme

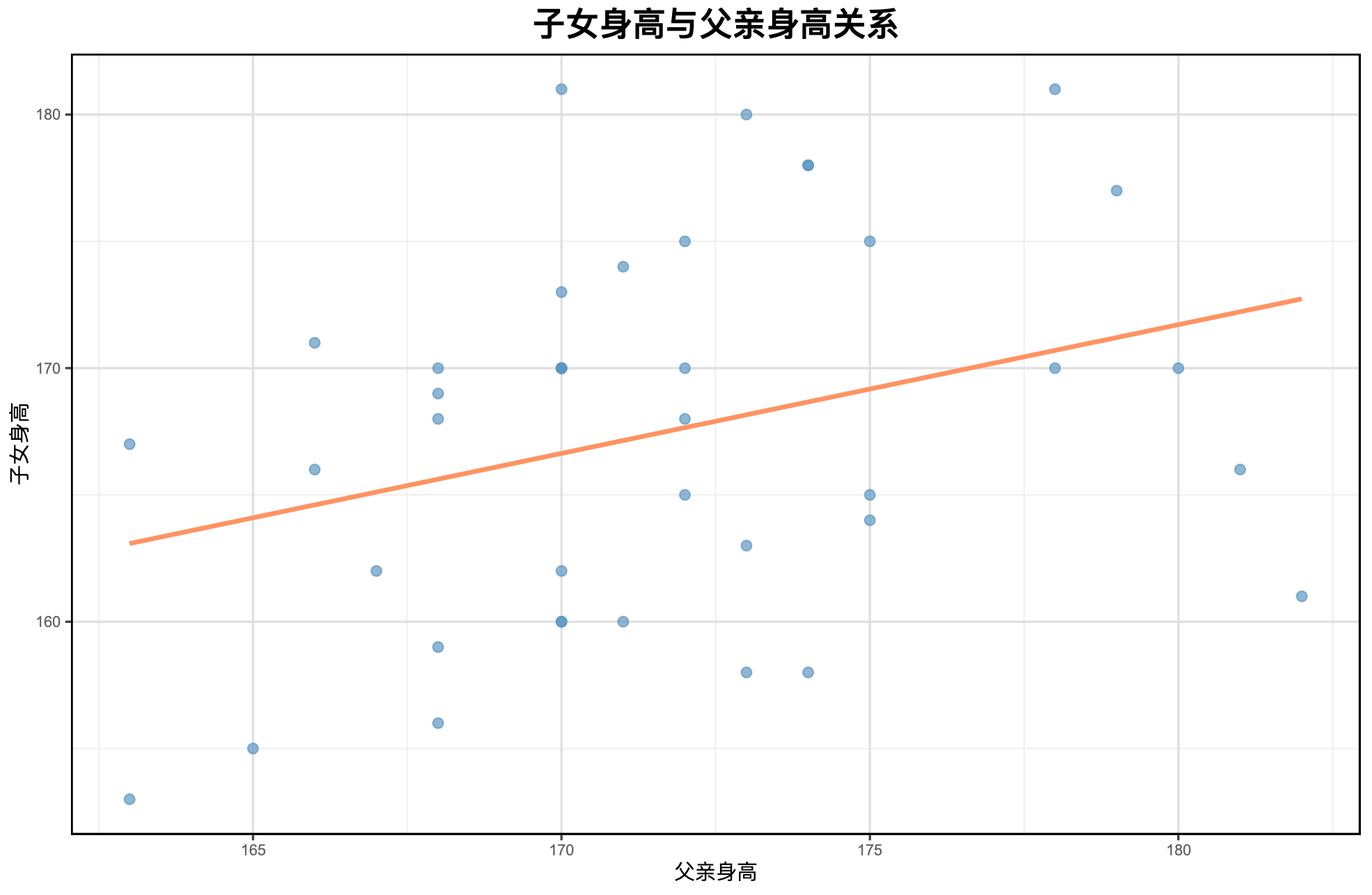
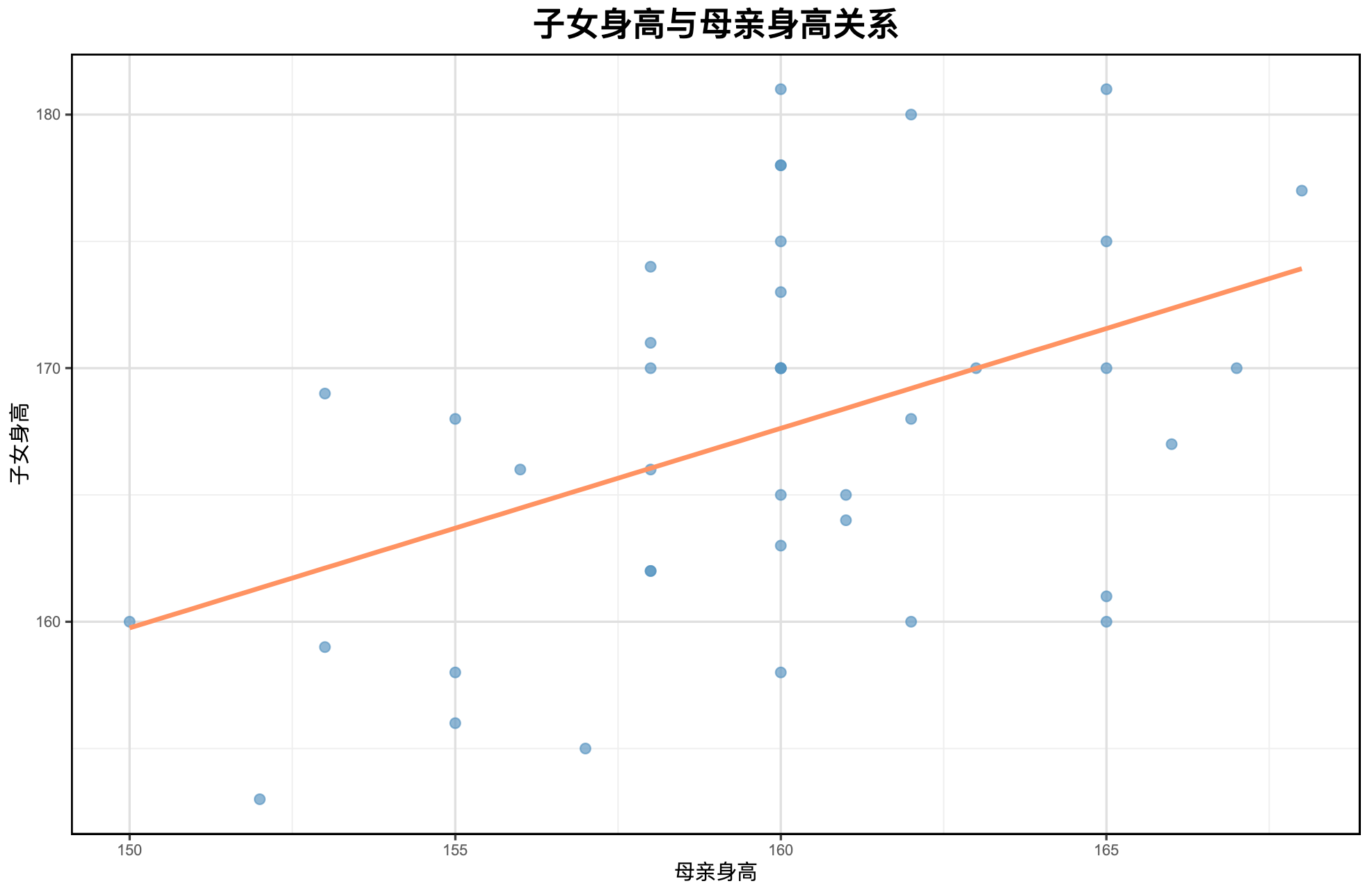
# 散点图

img.png

img.png
分别绘制子女身高与父亲身高和母亲身高的散点图，说明它们之间的关系。

1
2
3
4
5
6
7
8
9
10
11
12
13
# 子女 vs 父亲
ggplot(data, aes(x = father, y = children)) +
  geom_point(color = "steelblue", size = 2, alpha = 0.7) +
  geom_smooth(method = "lm", se = FALSE, color = "coral", linewidth = 1) +
  labs(title = "子女身高与父亲身高关系", x = "父亲身高", y = "子女身高") +
  mytheme

# 子女 vs 母亲
ggplot(data, aes(x = mother, y = children)) +
  geom_point(color = "steelblue", size = 2, alpha = 0.7) +
  geom_smooth(method = "lm", se = FALSE, color = "coral", linewidth = 1) +
  labs(title = "子女身高与母亲身高关系", x = "母亲身高", y = "子女身高") +
  mytheme

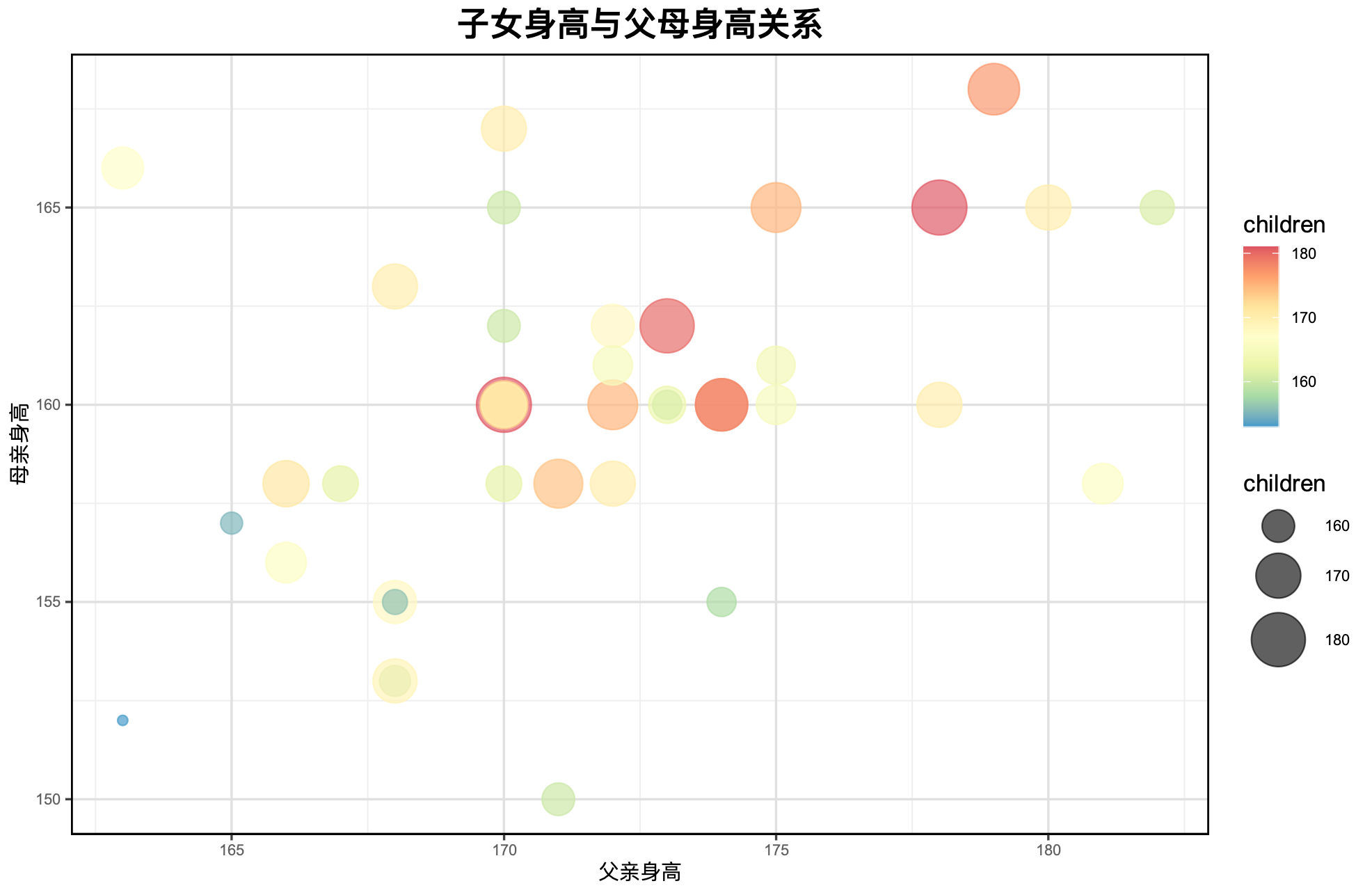
# 气泡图

以子女身高作为气泡大小，绘制气泡图，分析子女身高与父亲身高和母亲身高的关系。
img.png

1
2
3
4
5
6
7
8
9
ggplot(data, aes(x = father, y = mother,
                 size = children, color = children)) +
  geom_point(alpha = 0.7) +
  scale_color_distiller(palette = "Spectral") +
  scale_size(range = c(2, 12)) +
  labs(title = "子女身高与父母身高关系",
       x = "父亲身高", y = "母亲身高",
       size = "children", color = "children") +
  mytheme

# 描述性统计分析

1
2
# Exercise4_1 计算以下统计量，并进行分析
data1 <- read.csv("resources/data/exercise4_1.csv")

# 计算平均数、中位数、四分位数、第 80 百分位数和众数。

1
2
3
4
5
mean(data1$distribution.volume)
median(data1$distribution.volume)
quantile(data1$distribution.volume, probs = c(0.25, 0.75, 0.80), type = 7)
library(DescTools)
Mode(data1$distribution.volume)

展开输出

1
2
3
4
5
6
7
8
9
10
11
> mean(data1$distribution.volume)
[1] 24.80333
> median(data1$distribution.volume)
[1] 24.45
> quantile(data1$distribution.volume, probs = c(0.25, 0.75, 0.80), type = 7)
25%    75%    80%
22.750 26.875 27.300
> Mode(data1$distribution.volume)
[1] 22.7 22.9 25.0 25.9 27.3
attr(,"freq")
[1] 2

# 极差、四分位差、方差和标准差。

1
2
3
4
max(data1$distribution.volume) - min(data1$distribution.volume)
IQR(data1$distribution.volume, type = 7)
var(data1$distribution.volume)
sd(data1$distribution.volume)

# 偏度系数和峰度系数

1
2
3
library(e1071)
skewness(data1$distribution.volume, type = 2)
kurtosis(data1$distribution.volume, type = 2)

# 标准分数

1
as.vector(round(scale(data1$distribution.volume), 4))

指定 type=7 : m = 1-p. p[k] = (k - 1) / (n - 1).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# Exercise4_2 计算120家企业利润额的平均数和标准差（第一组和最后一组的组距根据相邻组确定）
data2 <- read.csv("resources/data/exercise4_2.csv")
# 计算平均数
wm2 <- weighted.mean(data2$group.median, data2$number.of.firms)
wm2
# 计算标准差
sumd2 <- sum((data2$group.median - wm2)^2 * data2$number.of.firms)
sqrt(sumd2 / (sum(data2$number.of.firms) - 1))

# Exercise4_3 依据15个工人分别用3种方法在相同时间内组装的产品数量
# 计算有关的描述统计量来评价组装方法的优劣
data3 <- read.csv("resources/data/exercise4_5.csv")
mean3 <- apply(data3, 2, mean)
sd3 <- apply(data3, 2, sd)
cv3 <- sd3 / mean3
df3 <- data.frame(平均数 = mean3, 标准差 = sd3, 变异系数 = cv3)
round(df3, 4)
# 依据结果，方法A的平均组装数量最高且变异系数最低，
# 说明方法A在效率和稳定性方面表现最好，因此方法A是三种方法中最优的组装方法。

# 推断的理论基础

# 正态分布相关计算 pnorm qnorm

  1. x~N(500, 202)

1
2
3
4
5
# P(X >= 510)
p1_1 <- 1 - pnorm(510, mean = 500, sd = 20)

# P(400 <= X <= 450)
p1_2 <- pnorm(450, mean = 500, sd = 20) - pnorm(400, mean = 500, sd = 20)

  1. Z~N(0, 1)

1
2
3
4
5
6
7
8
# P(0 <= Z <= 1.2)
p2_1 <- pnorm(1.2) - pnorm(0)

# P(0 <= Z <= 0.48)
p2_2 <- pnorm(0.48) - pnorm(0)

# P(Z >= 1.2)
p2_3 <- 1 - pnorm(1.2)

  1. 标准正态分布累积概率为 0.95 时的反函数值 z

1
z <- qnorm(0.95)

# t 分布相关计算 pt

1
2
3
4
5
6
7
8
9
10
11
# (1) X~t(df), df=15, P(t < -1.5)
df1 <- 15
pt1 <- pt(-1.5, df = df1)

# (2) df=20, P(t > 2)
df2 <- 20
pt2 <- 1 - pt(2, df = df2)

# (3) df=30, 右尾概率为0.05时的t值
df3 <- 30
t <- qt(0.95, df = df3)

# 两个总体检验

# 潜在购买力：t.test, paired, greater

某市场研究机构用一组被调查者样本来给某特定商品的潜在购买力打分。
样本中每个人都分别在看过该产品的新的电视广告之前与之后打分 (paired=TRUE) 。
潜在购买力的分值为 0~10 分，分值越高，表示潜在购买力越强。
原假设认为 “看后” 平均得分小于或等于 “看前” 平均得分，拒绝该假设就表示广告提高了平均潜在购买力得分 (alternative="greater") 。
设显著性水平 a=0.05 (conf.level=0.95) ，用下列数据检验该假设

1
2
3
4
5
exercise7_3 <- read.csv("../../resources/data/exercise7_3.csv")
t.test(exercise7_3$after, exercise7_3$before,
       paired = TRUE,
       alternative = "greater",
       conf.level = 0.95)

# 培训方法差异：t-test, two.sided

某企业为比较两种方法对员工培训的效果，采用方法 1 对 15 名员工进行培训，采用方法 2 对另外 15 名员工进行培训。
在 a=0.05 显著性水平下 (conf.level=0.95) ，检验两种方法的培训效果是否有显著差异 (alternative="two.sided") 。

1
2
3
exercise7_4 <- read.csv("../../resources/data/exercise7_4.csv")
method1 <- exercise7_4$method.1
method2 <- exercise7_4$method.2

  1. 假定方差相等 (var.equal=TRUE) 。

1
2
3
4
t.test(method1, method2,
       var.equal = TRUE,
       alternative = "two.sided",
       conf.level = 0.95)

  1. 假定方差不相等 (var.equal=FALSE) 。

1
2
3
4
t.test(method1, method2,
       var.equal = FALSE,
       alternative = "two.sided",
       conf.level = 0.95)

  1. 计算效应量，分析差异程度 cohensD

1
cohensD(method1, method2, method = "pooled")

# 认知的性别差异：显著性检验的手算方法

为研究小企业经理对自身成功与否的认知是否存在性别差异，随机抽取了 100 名女性经理和 95 名男性经理进行调查。
结果显示：女性经理中认为自已成功的人数为 24 人，男性经理中认为自己成功的人数为 39 人。
在 a=0.05 的显著性水平下，检验男女经理认为自己成功的人数比例是否有显著差异。

1
2
3
4
5
6
7
8
9
10
n1 <- 100
x1 <- 24
n2 <- 95
x2 <- 39
p1 <- x1 / n1
p2 <- x2 / n2
pd <- (x1 + x2) / (n1 + n2)
z <- (p1 - p2) / sqrt(pd * (1 - pd) * (1 / n1 + 1 / n2))
p_val <- 2 * (1 - pnorm(abs(z)))
data.frame(z, p_val)

# 新旧肥料差异：t-test, 综合

为比较新、旧两种肥料对产量的影响，以便决定是否采用新肥料，
研究者选择了面积相等、土壤等条件相同的 40 块田地，分别施用新、旧两种肥料 (paired=FALSE) ，
得到的产量数据 (单位：千克) 如下 (exercise7_7)。

1
2
3
exercise7_7 <- read.csv("../../resources/data/exercise7_7.csv")
old <- exercise7_7$old
new <- exercise7_7$new

设显著性水平 a=0.05:

  1. 假定方差相等 (var.equal) ，检验施用新肥料获得的平均产量是否显著高于 (greater) 旧肥料。

1
2
3
4
t.test(new, old,
       var.equal = TRUE,
       alternative = "greater",
       conf.level = 0.95)

  1. 检验两种肥料产量的方差是否有显著差异 (two.sided) 。

1
2
3
var.test(new, old,
         alternative = "two.sided",
         conf.level = 0.95)

  1. 计算效应量，分析差异程度。

1
cohensD(new, old, method = "pooled")

# 置信区间与均值检验

# 地铁通勤时间：已知 σ 与未知 σ 下均值区间

为调查每天上班乘坐地铁所花费的时问，在某城市乘坐地铁的上班族中随机抽取 50 人，得到他们每天上班乘坐地铁所花费的时间数据如下 (
单位：分钟) (exercise5_4$time)。
计算乘坐地铁平均花费时间的置信区间:

  1. 假定总体标准差为 20 分钟 (sigma.x=20) ，置信水平为 95% (conf.level=95) 。
  2. 假定总体标准差未知，置信水平为 90%。

1
2
z.test(exercise5_4$time, sigma.x = 20, conf.level = 0.95)
t.test(exercise5_4$time, conf.level = 0.90)

# PM2.5: 均值区间 + 单侧检验

为监测空气质量，某城市环保部门每隔几周对空气烟尘质量进行一次随机测试已知该城市过去每立方米空气中 PM2.5 的平均值是 82 微克。在最近一段时间的检测中 PM2.5 的数值如下 (
单位：微克) (exercise5_5$PM2.5)

  1. 构建 PM2.5 均值的 95% (conf.level=0.95) 的置信区间:
  2. 根据最近的测量数据，当显著性水平 a=0.05 时，能否认为该城市空气中 PM2.5 的平均值显著低于 (alternative='less') 过去的平均值

1
2
3
4
5
6
exercise5_5 <- read.csv("resources/data/exercise5_5.csv")
# (1)构建PM2.5均值的95%的置信区间:
z.test(exercise5_5$PM2.5, sigma.x = sd(exercise5_5$PM2.5), conf.level = 0.95)
# (2)根据最近的测量数据，当显著性水平a=0.05时，能否认为该城市空气中PM25的平均值显著低于过去的平均值
z.test(exercise5_5$PM2.5, mu = 82, sigma.x = sd(exercise5_5$PM2.5),
       alternative = "less", conf.level = 0.95)

# 金属板重量：均值区间 + 双侧检验（μ=25）

安装在一种联合收割机上的金属板的平均重量为 25kg。对某企业生产的 20 块金属板进行测量，得到的重量数据如下（exercise5_6$Weight)。

  1. 假设金属板的重量服从正态分布，构建该金属板平均重量的 95% 的置信区间。
  2. 检验该企业生产的金属板是否符合要求。假设总体方差为 5kg，a=0.01; 假设总体方差未知，a=0.05。

1
2
3
4
5
6
exercise5_6 <- read.csv("resources/data/exercise5_6.csv")
z.test(exercise5_6$Weight, sigma.x = sd(exercise5_6$Weight), conf.level = 0.95)
z.test(exercise5_6$Weight, mu = 25, sigma.x = sqrt(5),
       alternative = "two.sided", conf.level = 0.99)
t.test(exercise5_6$Weight, mu = 25,
        alternative = "two.sided", conf.level = 0.95)

# 比例右尾：早餐牛奶比例检验，手算 z 值与 p 值。

对消费者的一项调查表明，17% 的人早餐饮料是牛奶。

某城市的牛奶生产商认为，该城市的人早餐饮用牛奶的比例更高。

为验证这一说法，生产商随机抽取 550 人的一个随机样本，其中 115 人早餐饮用牛奶。

在 a=0.05 显著性水平下，检验该生产商的说法是否属实。

1
2
3
4
5
6
7
n <- 550
x <- 115
p <- x / n    # 样本比例
pi0 <- 0.17
z <- (p - pi0) / sqrt(pi0 * (1 - pi0) / n)  # 计算检验统计量
p_val <- 1 - pnorm(z)  # 计算p值（右尾检验）
data.frame(z, p_val)

z.test 有两种写法（分别来自 BSDA 和 TeachingDemos ）:
主要区别：前者可选双样本的 z 检验，标准差参数名为 sigma.x(y) ；后者只可用于单样本，标准差参数名为 stdev .

# 方差分析练习

# 机器装填量：单因素 ANOVA、效应量、HSD 事后比较，箱线图与目标线。

一家牛奶公司有 4 台机器装填牛奶，每桶的容量为 4L。
下面是从 4 台机器中抽取的装填量 (单位：L) 样本数据
数据：exercise9_1 （包含 4 台机器 6 次抽取的数据）

  1. 检验机器对装填量是否有显著影响 (α=0.01)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
library(reshape2)
library(ggpubr)

data <- read.csv("../../resources/data/exercise9_1.csv", header = TRUE)

data_long <- melt(data, variable.name = "机器", value.name = "装填量")

aov_model <- aov(装填量 ~ 机器, data = data_long)

# 单因素方差分析结果
summary(aov_model)

alpha <- 0.01
f_value <- summary(aov_model)[[1]]$`F value`[1]
p_value <- summary(aov_model)[[1]]$`Pr(>F)`[1]

# 检验结论
cat(sprintf("F统计量 = %. 4f\n", f_value, "p值 = %. 4f\n", p_value))

boxplot(装填量 ~ 机器, data = data_long,
        main = "各机器装填量箱线图",
        xlab = "机器", ylab = "装填量(L)",
        col = c("#FFB6C1", "#87CEEB", "#98FB98", "#FFD700"))
abline(h = 4, col = "red", lty = 2, lwd = 2)

  1. 分析效应量。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
library(DescTools)

aov_model <- aov(装填量 ~ 机器, data = data_long)

eta_squared <- EtaSq(aov_model, type = 1)

# 效应量分析
cat("Eta Squared (η²):\n", eta_squared[1, 1])

means <- tapply(data_long$装填量, data_long$机器, mean)
sds <- tapply(data_long$装填量, data_long$机器, sd)

# 各机器描述性统计
stats_df <- data.frame(
  机器 = names(means),
  mean = means,
  sd = sds
)
print(stats_df, row.names = FALSE)

  1. 采用 HSD 方法比较哪些机器的装填量之间存在显著差异

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
library(agricolae)
library(ggpubr)

aov_model <- aov(装填量 ~ 机器, data = data_long)

hsd_result <- HSD.test(aov_model, "机器", alpha = 0.01)

cat("Tukey HSD多重比较结果(α=0.01)：\n\n")
cat("各组均值和分组：\n")
print(hsd_result$groups)

cat("\n\n成对比较详细结果：\n")
tukey_detailed <- TukeyHSD(aov_model, conf.level = 0.99)
print(tukey_detailed)

cat("\n\n显著差异总结：\n")
comparison_matrix <- tukey_detailed$机器
sig_diff <- comparison_matrix[comparison_matrix[, "p adj"] < 0.01, ]

plot(tukey_detailed, las = 1, col = "steelblue")
abline(v = 0, col = "red", lty = 2, lwd = 2)

# 管理者满意度：单因素 ANOVA，HSD，正态性 (Q-Q、Shapiro)，方差齐性 Levene。

一家管理咨询公司为不同的客户提供人力资源管理讲座。

每次讲座的内容基本上一样，听课者有时是高层管理者，有时是中层管理者，有时是基层管理者。

该咨询公司认为，不同层级的管理者对讲座的满意度是不同的。

听完讲座后随机抽取不同层级的管理者，其满意度评分如下 (评分标准是 1~10 分，10 分代表非常满意)。

1
2
3
4
library(reshape2)
exercise9_2 <- read.csv("../../resources/data/exercise9_2.csv")
table9_2 <- melt(exercise9_2, variable.name = "管理者层级", value.name = "满意度评分")
table9_2

  1. 检验管理者的层级不同是否会导致评分的显著差异 (a=0.05) 并分析效应量。

1
2
3
4
5
library(DescTools)
model_1w <- aov(满意度评分 ~ 管理者层级, data = table9_2)
summary(model_1w)
EtaSq(model_1w)

  1. 采用 HSD 方法比较管理者的评分之间的差异。

1
2
3
library(agricolae)
HSD.test(model_1w, "管理者层级", group=TRUE, console=TRUE)

  1. 检验满意度评分是否满足正态性和方差齐性。

1
2
3
4
5
6
7
8
9
library(car)
# 正态性检验
qqnorm(table9_2$满意度评分)
qqline(table9_2$满意度评分, col="red", lwd=2)
shapiro.test(table9_2$满意度评分)

# 方差齐性检验
leveneTest(满意度评分 ~ 管理者层级, data = table9_2)

# 路段 × 时段：双因素 ANOVA（主效应 + 交互），偏效应量。

城市道路交通管理部门为研究不同路段和不同时间段对行车时间的影响，让一名交通警察分别在 3 个路段的高峰期与非高峰期亲自驾车进行实验，
通过实验共获得 30 个行车时间 (单位：分钟) 数据，如下所示。

1
2
3
exercise9_5 <- read.csv("../../resources/data/exercise9_5.csv")
table9_5 <- melt(exercise9_5, id.vars="时段", variable.name = "路段", value.name = "行车时间")
table9_5

  1. 分析路段、时段以及路段和时段的交互作用对行车时间的影响 (α =0.05)

1
2
3
4
5
6
7
8
library(DescTools)
model_road <- aov(行车时间 ~ 路段, data = table9_5)
summary(model_road)
model_time <- aov(行车时间 ~ 时段, data = table9_5)
summary(model_time)
model_interaction <- aov(行车时间 ~ 路段 * 时段, data = table9_5)
summary(model_interaction)

  1. 计算偏效应量并进行分析。

1
2
3
4
library(DescTools)
EtaSq(model_road)
EtaSq(model_time)
EtaSq(model_interaction)

# 相关与回归练习

  • 相关与可视化：散点 + 边际箱线，皮尔逊相关。
  • 多元回归：每股收益～多指标，系数区间、方差分析、标准化系数、VIF、逐步回归，诊断与预测区间。

# 一元回归：航班准点率→投诉次数，系数检验、预测、置信 / 预测区间。

随机抽取 10 家航空公司，对其最近一年的航班准点率和顾客投诉次数进行调查，所得数据如下 (exercise10_2)。

1
2
exercise10_2 <- read.csv("../../resources/data/exercise10_2.csv")
exercise10_2

  1. 用航班准点率作为自变量，顾客投诉次数作为因变量，求出估计的回归方程，并解释回归系数的意义。

1
2
3
# 一元线性回归模型
model <- lm(投诉次数 ~ 航班准点率, data = exercise10_2)
summary(model)

  1. 检验回归系数的显著性 (x=0.05)

1
2
3
4
5
# 计算回归系数的置信区间
print(confint(model, level = 0.95), digits = 4)

# 输出方差分析表
anova(model)

  1. 如果航班准点率为 80%，估计顾客的投诉次数、预测区间及置信区间

1
2
3
4
# 计算x0=80时投诉次数的点预测值及其置信区间和预测区间
x0 <- data.frame(航班准点率 = 80)
predict(model, x0, interval = "confidence", level = 0.95)
predict(model, x0, interval = "prediction", level = 0.95)

更新于

请我喝[茶]~(￣▽￣)~*

梦前辈 微信支付

微信支付

梦前辈 支付宝

支付宝